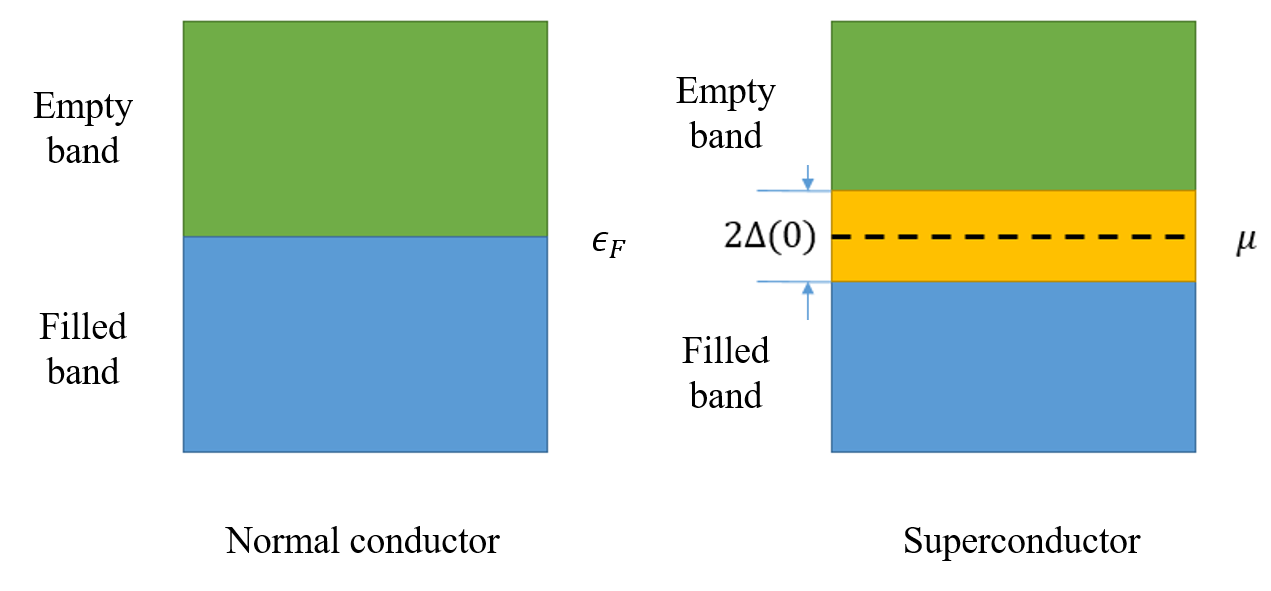
Superconducting Energy Gap
BCS theory predicts
\[ k_BT_C=1.14\hbar\omega_De^{-1/N(0)V} \]
\[ 2\Delta(0)=3.53 k_BT_C \]
where \(T_C\) is the critical temperature of a superconductor, and \(\Delta\) is the superconducting energy gap.
Models on Normal State & Superconductor Junction
- Andreev Reflection
- B. T. K Model

Andreev Reflection

B.T.K Model
\[ \text{Andreev Reflection} \stackrel{Z\neq0}{\longrightarrow} \text{B. T. K Model} \]
where \(Z\) is the effective barrier.



PCS Experimental Setup

Result